17.3 Surface area and volume of cubes
A cube is a solid with six identical square faces at right angles to each other.
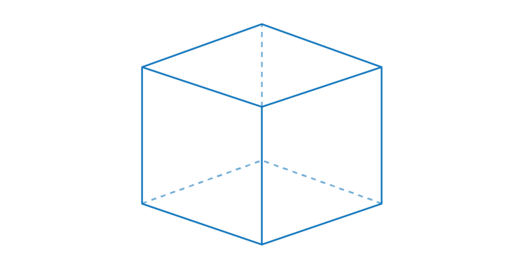
Calculating surface area of a cube
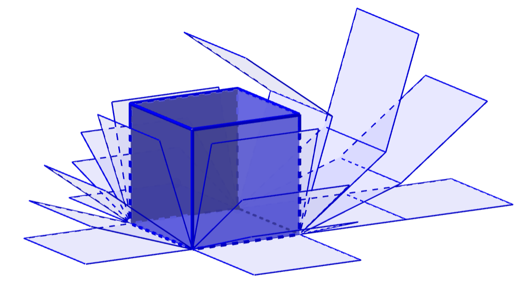
A cube unfolded into a net is made up of six identical squares.

Worked Example 17.1: Calculating the surface area of a cube
Calculate the surface area of the cube.
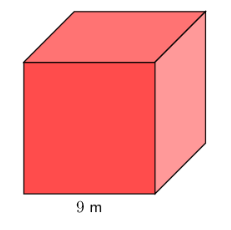
Determine the area of one square face and multiply by six.
A cube has six identical square faces. We must calculate the area of one face and multiply it by six to get the total surface area of the cube.
\[\begin{align} \text{Surface area} &= 6 \times \text{area of square face} \\ &= 6 \times (9 \times 9) \\ &= 6 \times 81 \\ &= 486 \end{align}\]Write the final answer.
Give the answer using the correct units. The diagram gives the measurement in metres, and the units of surface area are square units.
\[\text{Surface area of cube} = 486 \text{ m}^2\]Worked Example 17.2: Finding the length of cube from the surface area
The surface area of the cube is \(294 \text{ cm}^2\). Find the length \(x\) of the cube.
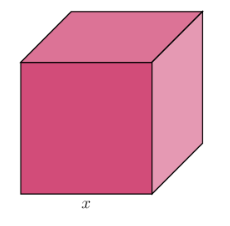
Determine the length of the cube using formula for surface area.
\[\begin{align} \text{Surface area} &= 6 \times \text{area of square face} \\ 294 &= 6 \times (x \times x) \\ 294 &= 6 \times x^2 \\ \frac{294}{6} &= \frac{6x^2}{6} \\ 49 &= x^2 \\ \sqrt{49} &= x \\ 7 &= x \end{align}\]Write the final answer.
\[\text{Length of cube } x = 7 \text{ cm}\]Calculating volume of a cube
We use this formula to calculate the volume of a cube:
\[\begin{align} \text{Volume of cube} &= \text{length} \times \text{breadth} \times \text{height} \\ &= l^3 \\ \end{align}\]We can also express the formula for the volume of a cube as the product of the area of the base and the height of the cube.
\[\text{Volume of cube} = \text{(area of the base)} \times \text{height}\]Worked Example 17.3: Calculating the volume of a cube
Find the volume of the cube with \(l = 3 \text{ cm}\).
Write down the formula for the volume of a cube.
\[\text{Volume} = l^3\]Calculate the volume of the cube.
\[\begin{align} \text{Volume} &= l^3 \\ &= 3^3 \\ &= 27 \end{align}\]Write the final answer.
When you write down the final answer, always remember to give the correct units.
The volume of the cube is \(27 \text{ cm}^3\).
