7.2 Set up, analyse and interpret algebraic equations
An equation is a mathematical sentence that is true for some numbers, but false for other numbers. The following are examples of equations: \(x + 3 = 11\) and \(2^{x} = 8\).
- \(x + 3 = 11\) is true if \(x = 8\), but false if \(x = 3\).
- \(2^{x} = 8\) is true if \(x = 3\), but false if \(x = 5\).
When we look for a number or numbers that make an equation true, we say that we are solving the equation or looking for a solution to an equation. For example, \(x = 4\) is the solution of \(2x = 8\) because it makes \(2x = 8\) true. (Check: \(2 \times 4 = 8\))
- equation
- a mathematical sentence with an equals sign
- solution to an equation
- a number that makes the equation true when you substitute it for the variable
It is sometimes helpful to read or write the equation in words using “a number” in place of the letter symbol \(x\), and then work out what you think “the number” is in each case.
For example: \(4 + x = 20\). Four plus “a number” equals twenty.
The number is \(16\), because \(4 + 16 = 20\). This means \(x = 16\) is a solution of the equation \(4 + x = 20\).
An equation in mathematics can be compared to a balance scale. The fulcrum in a balance scale is at the exact centre of the bar. In mathematics, this can be compared to the equals sign. Everything on the left side of the equation must be equal to everything on the right side of the equation, just like a balance scale.

The equation for this balance scale is \(t + 9 = 22\) and to balance it we need \(t = 13\), because \(13 + 9 = 22\).
Worked Example 7.1: Setting up equations
The balance scale below is balanced. That means it has the same weight on both sides.
Write down the equation represented by this balanced scale.

Write down the equation.
This scale is in balance, so the right-hand side is equal to the left-hand side. So, something = something else. The equation should look like this: \(q + 69 = 9\).
You shouldn’t worry that there is a bigger number on the left of the scale and a smaller number is on the right side. The letter \(q\) will balance the equation, once you work out what value must replace it.
To keep the balance scale balanced without tipping it to the left or right, we must make sure that the letter \(q\) is replaced by the correct number.
\[69 - 60 = 9\]This is the same as
\[\mathbf{- 60} + 69 = 9\]Can you see that \(q\) must be equal to \(- 60\)?
Worked Example 7.2: Setting up equations
Is \(x = 7\) a solution to the following equation?
\[7x = 63\]Substitute \(7\) into the equation.
Left-hand side of the equation has \(x\), so substitute: \(7(7)\)
\[\begin{align} 7(7) &= 49 \\ 49 &\neq 63 \end{align}\]Check the balance scale.
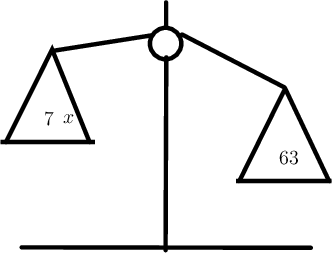
The scale is not balanced. The expression on the left is smaller than the expression on the right.
From the above calculation we can see that \(x = 7\) is not a solution to the equation.
Worked Example 7.3: Setting up equations
Is \(m = 8\) a solution to the following equation?
\[m + m = 16\]Substitute \(8\) into the equation.
Left-hand side of the equation has \(m\), so substitute: \(8 + 8\)
\[\begin{align} 8 + 8 &= 16 \\ 16 &= 16 \end{align}\]Check the balance scale.
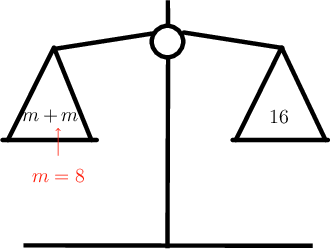
The scale is balanced! So, the expression on the left is equal to the expression on the right.
\[(8) + (8) = 16\]From the above calculation, we can see that that \(m = 8\) is a solution to the equation.
